대학원 수업 'Deep Learning', 교재 'Understanding Deep Learning', 그리고 직접 찾아서 공부한 내용들을 토대로 작성하였습니다.
deep neural network의 특징 중 하나는 너무 많은 layer를 쌓으면 performance가 줄어든다는 점입니다.
이 챕터에선 이를 해결하는 'residual blocks'에 대해 알아보겠습니다.
여기서, 각 layer는 직접적으로 변형하는 대신 현재 representation에 대해 추가적인 변화를 계산합니다. 이는 더 깊은 network가 train되도록 하지만 초기화에서 기하급수적인 크기로 증가할 수 있게 만듭니다.
Residual block은 이런 현상을 보완하기 위해 'batch normalization'을 사용합니다.
batch normalization을 사용하는 residual block 더 깊은 network에서도 잘 train되고, 다양한 task에서 성능을 향상시킵니다.
Sequential processing

지금까지 봐온 모든 network는 data가 순차적으로 진행됩니ㅣ다. 각 layer는 이전 layer의 output을 받고 그 다음 layer에 전달합니다.
h1=f1[x, Φ1]
h2=f2[h1, Φ2]
h3=f3[h2, Φ3]
y=f4[h3, Φ4]
기존의 neural network에서, 각 layer는 activation function을 지나는 linear transformation으로 구성이되고, parameter Φ(k)는 linear transformation의 weight와 bias로 구성됩니다.
convolutional network에선, 각 layer가 activation function을 지나는 convolution의 set으로 구성되고, parameter는 convolutional kernel과 bias로 구성됩니다.
processing은 연속적이기 때문에, 우리는 network를 중첩된 function들의 연속이라고 볼 수 있습니다.

Limitations of sequential processing

위 figure에서 볼 수 있듯 우리는 분명 capacity가 더해지면 일반적으로 성능이 더 좋다는 것을 봤습니다. 그리고 convolutional network를 다루면서 (AlexNet->VGG) 많은 later를 쌓을수록 convolutional network는 더 성능이 좋아진다는 것도 확인했습니다.

그러나 훨씬 더 많은 layer를 쌓게 된다면, 다시 성능을 줄어듭니다.
실제로 이 현상을 test 뿐만 아니라 training도 해당됩니다. 즉, generalize의 문제가 아니라 'deeper network를 training' 하는 것이 문제라는 것을 의미합니다.
이런 현상은 왜 일어날까요?
1. initialization에서, early network layer의 parameter를 수정할 때, loss gradient는 예상치못하게 변합니다. 물론, 적절한 initialization에선, parameter에 대한 loss의 gradient가 exploding이나 vanishing gradient 문제 없이 잘 작동할 겁니다. 그러나 만약 derivative가 parameter에 대해 infinitesimal하게 변한하고, optimization algorithm은 finite step size를 사용한다고 가정해봅시다. 어떠한 step size를 사용해도 완전히 다르고 관련없는 gradient로 가게 될 것입니다. loss surface는 하나의 smooth한 구조가 아닌 엄청 많은 작은 산들이 있는 형태로 (뒤죽박죽) 나타날 것입니다.
shallow network에선, input에 대한 output의 gradient가 우리가 input을 바꿔도 천천히 바뀝니다. 그러나 deep network에선, input에 작은 변화만 줘도 완전히 다른 gradient가 됩니다.

a) hidden layer가 1일 때, gradient가 smooth하게 변합니다. 즉, correlation이 강합니다 (1에 가까움).
b) hidden layer가 24일 때엔, input가 조금만 변해도 gradient가 크게 진동합니다. 즉, correlation이 약합니다. (0에 가까움)
c)는 gradient의 autocoorrelation function입니다. x가 조금만 변해도 24hidden layers는 급격히 correlation이 0이 됩니다.
가까운 gradient는 shallow network에ㅔ correlated 되어 있지만, 이 correlation은 deep network를 빠르게 0으로 떨어뜨립니다. 이런 현상을 "shattered gradients"라고 합니다.
이런 현상이 나타나는 이유는, network가 깊어질수록 초기의 network later들의 변화가 output을 점점 복잡하게 바꾸기 때문입니다. first layer에 대한 output y의 derivative는 다음과 같이 표현할 수 있습니다.
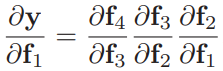
우리가 만약 f1을 결정하는 parameter를 바꾼다면, 여기에 차례로 있는 모든 derivative가 바뀔 수 있습니다. (f2,f3,f4는 f1으로부터 계산된 것이기 때문)
결론적으로 각 training example에서 update된 gradient는 완전히 다를 것이고, loss function은 바람직하지 않게 표현될 것입니다.
Residual connections and residual blocks
'Residual' 혹은 'skip connections'는 computational path의 branch입니다.
각 layer f[.]에 들어가는 input이 실제 output에 추가되는 과정입니다.
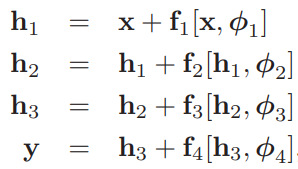
오른쪽 항의 첫번째 term이 residual connection이 됩니다. 이렇게 되면 각 function fk는 현재 representation에서 추가적인 변화도 학습할 수 있게 됩니다. 이를 만족하기 위해선 output의 size와 input의 size가 동일해야만 합니다. input과 이렇게 진행된 output의 추가적인 combination을 우리는 'residual block' 혹은 'residual layer'라고 부릅니다.
이 식을 우리는 각각 대입해 하나의 식으로 정의할 수도 있습니다.
- intermediate quantities hk:
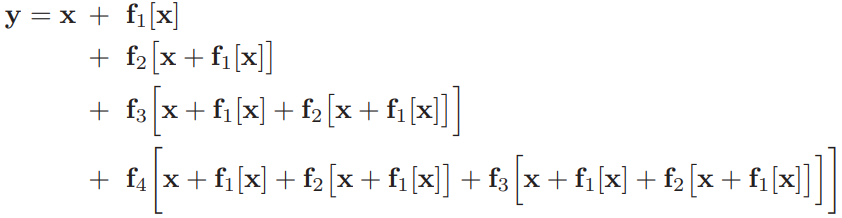
여기서 final network output은 input과 더 작은 4개의 network의 합으로 표현됩니다.
우리는 이 식을 network를 "unraveling(풀림)" 한다고 합니다.
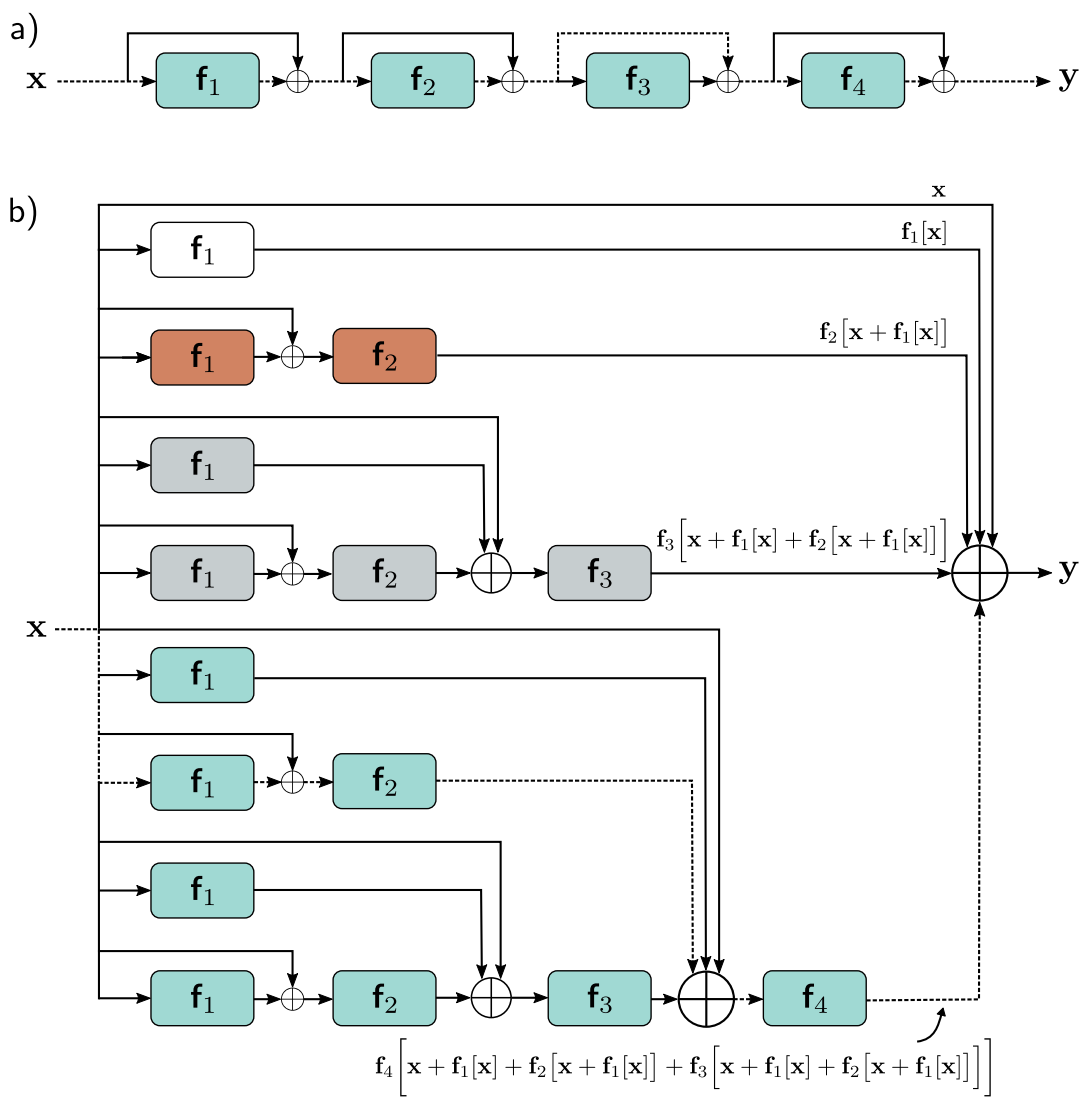
residual connections은 original network를 더 작은 network의 앙상블로 바꿨다고 볼 수 있습니다. (result 계산하기 위해 output이 합쳐짐)
또한, residual network는 input에서 output까지 다른 길이의 16개의 path를 만든다고 볼 수도 있습니다. f1[x]를 보면 직접적은 additive term을 포함한 8개의 path에 존재합니다.
즉, f1에 대한 y의 derivative는

이렇게 됩니다.
Order of operations in residual blocks
지금까진 additive functions f[x]가 어떤 network later도 가능하다고 가정했습니다. 물론 사실이지만, function에 operation의 순서는 매우 중요합니다. function은 ReLU와 같은 nonlinear activation function이 포함되어 있거나, 전체 network가 linear할 수 있습니다.
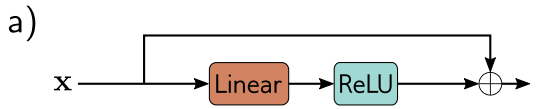
그러나 전형적인 network layer에선, ReLU function은 끝에 있고, 그렇기 때문에 output은 non-negative입니다. 만약 이 convention을 사용한다면, 각 residual block은 input value를 증가시키기만 합니다.

이를 방지하기 위해, 보통 operation의 순서를 바꿔서 activation function이 먼저 적용되도록 하고, 그다음 linear transformation을 합니다. 근데 이때 시작을 activation으로 한다고 가정했을 때, initial network input이 negative라면 ReLU로 인해 모든 signal이 0이 됩니다. 그러므로, 보통 시작을 linear transformation으로 하게 됩니다.

가끔은 이 그림처럼 residual block안에 여러 layer가 동작할 수 있습니다.
Deeper networks with residual connections
residual connection을 추가하면 performance가 저하되기 전에 보통 훈련할 수 있는 network의 depth가 약 2배 증가합니다. 하지만 residual connection으로 깊이를 임의로 더 늘릴 순 없습니다. 이 이유를 이해하기 위해선, forward pass 중에 activation의 variance가 어떻게 변하고, backward pass 중에 gradient크기가 어떻게 변하는지 고려해야 합니다.
Exploding gradients in residual networks
initialization에 따라, forward pass 하는 동안 중간 값의 크기가 매우 커지거나 작아질 수 있고, backward pass에서도 explode하거나 vanish할 수 있습니다.
그렇기 때문에 forward pass에선 activation의 expected variance를, backward pass에선 gradient는 layer사이에서 동일하도록 초기화합니다.
그렇다면 residual network를 생각해봅시다.
network output에 직접적으로 영향을 줄 수 있는 path가 있기 때문에 network depth에 대해 중간 값이나 vanishing gradient는 걱정할 필요는 없습니다. 하지만, 우리가 residual block에서 He initialization를 써도, network를 지나가며 forward pass의 value는 급격하게 증가합니다.
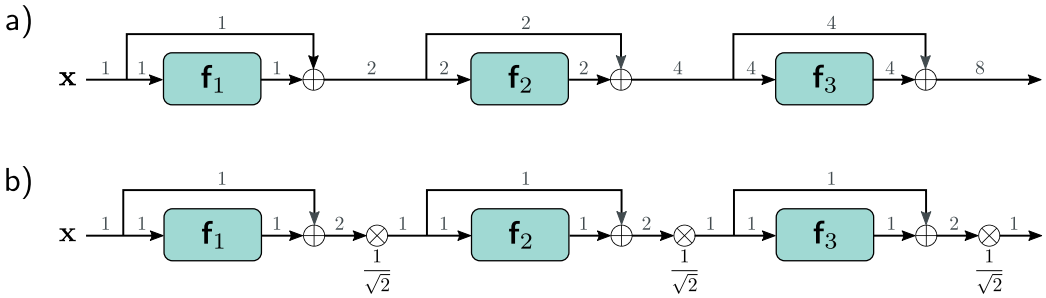
이유를 살펴보자면, residual block의 처리 결과를 input에 다시 추가해봅시다. 각 branch는 uncorrelated variability를 갖습니다.
(a) 그러므로, 다시 결합시키면 전반적인 variance는 증가합니다. ReLU activation과 He initialization을 사용하면, expected variance는 각 block의 처리에 의해 변하지 않습니다. forward pass에서 floating point precision 전에 가능한 network depth를 제한합니다. backpropagation의 backward pass에서 gradient에도 비슷한 argument가 제안합니다.
residual은 He initialziation을 사용해도 불안정한 forward propagation과 exploding gradient가 여전히 존재합니다.
(b) 이런 pass를 안정시킬 수 있는 방법 중 하나는 He initialization를 사용하고 doubling을 보상하기 위해 각 residual block의 결합된 output에 1/(2^1/2)를 곱하면 됩니다.
(c) 그러나 'batch normalization'을 사용하는 것이 더 유용합니다.
Batch normalization
Batch normalization 논문에서는 불안정한 learning이 일어나는 이유가 각 layer나 activation마다 input의 variance가 달라지는 'internal covariance shift' 때문이라고 주장합니다.
Batch normalization 혹은 BatchNorm은 batch B가 training동안 학습하는 value에 대한 mean과 variance 각 activation h를 shift하고 rescale합니다. 먼저, empirical mean m(h)과 standard deviation s(h)는 계산됩니다.

모든 값이 scalar입니다. batch activation이 mean zero와 unit variance를 갖도록 이 statistics를 사용합니다.

여기서 epsilon은 만약 h(i)가 batch의 모든 mbemer와 같아서 s(h)=0이 되면 이 때 0으로 나누는 것을 방지하기 위한 작은 수 입니다.
마지막으로, normalized된 variable은 gamma로 scaling되고 delta에 의해 shifted됩니다.

이 operation을 진행한 후, activation은 batch의 모든 member에 대한 mean delta와 standard deviation gamma를 갖게 됩니다. 이 두 값은 training동안 학습됩니다,
Batch normalization은 각 hidden unit에 따라 독립적으로 적용됩니다. K개의 layer를 가진 standard neural network에서, 각 D개의 hidden units를 갖고 있다면, offset delta를 훈련하는 KD와 scales gamma를 훈련하는 KD가 있을 것입니다. convolutional network에서, normalizing statistics는 batch와 spatial position 모두에서 계산됩니다. 만약 K개의 layer가 있고, 각각은 C channel를 포함하고 있다면, KC offset과 KC scale이 있을 것입니다. test 할 땐, 우린 statistics를 얻을 수 있는 batch가 없습니다. 이를 해결하기 위해, statistics m(h)와 s(h)는 전체 training dataset를 통해 계산되고 마지막 network에서 동결됩니다.

먼저 residual block에서 batch normalization을 하고 연관된 offset delta를 zero로, gamma를 1로 초기화시킵니다. 이는 각 layer의 input이 unit variance를 갖도록 바꾸고, He initialization과 함께, output variance도 1이 될 것입니다. 이제 variance는 residual block의 수에 따라 선형적으로 증가합니다. 단점은, initializatio에서, 이후의 network layer는 residual connection에 의해 지배되고 그래서 identity를 계산하는 것과 가까워집니다.
Costs and benefits of batch normalization
Batch normalization은 network가 각 activation에 기여하는 weight와 bias를 재조정하는 데 변하지 않도록 합니다. batch norm이 double이 되면, activation도 double이 되고, estimated standard deviation s(h)도 double이 되고, normalization은 이런 변화들을 메워줄 겁니다. 이는 각 hidden unit마다 별도로 일어납니다. 결과적으로, 모두 같은 효과를 주는 weight와 bias의 large family가 생깁니다. Batch normalization은 각 hidden unit마다 model를 어쨌든 크게 만드는 2개의 parameter gamma와 delta를 추가합니다.그러므로, 이 둘은 모두 weight parameter에서 redundancy를 만들고, 이런 redundancy를 보상하기 위해 추가적은 parameter를 추가합니다. 비효율적이지만, batch normalization은 여러 장점이 있습니다.
- Stable forward propagation
offset delta를 0으로, scale gamma를 1로 초기화하면 각 output activatin은 unit variance를 가집니다. regular network에서, 이는 initialization에서 forward propagation하는 동안 variance가 안정적이게 됩니다. residual network에선 각 layer의 input에 variation의 새로운 source를 추가하기 때문에 variance는 증가할 수밖에 없습니다. k번째 layer에서 기존의 k variance에 one unit variance를 추가하게 됩니다. (위의 c figure에 나와있는 내용입니다)
초기화할 때, later layer가 earlier layer에 비해 전반적인 variation에 더 적은 변화를 주는 단점이 있습니다. later layer은 identity를 계산하는 것과 가깝기 때문에 training 초기에 덜 깊습니다.
training 하는 동안, network는 이후 layer에서 scales gamma를 증가시키고 자체적으로 effective depth를 control할 수 있습니다.
- Higher learning rates
batch norm은 loss surface와 gradient를 더 smooth하게 만들어줍니다. 이는 surface를 조금 더 예측가능하게 만들기 때문에 더 높은 learning rate를 사용할 수 있습니다.
- Regularization
normalizaiton은 batch statistics에 의존하기 때문에 batch norm은 noise를 주입합니다. 주어진 traininig example을 위한 activation은 batch의 다른 member에 의해 normalize되고, 각 training iteration마다 조금씩 다를 것입니다.
Common residual architectures
Residual connection은 deep learning pipline에서 빠질 수 없는 부분이 됐습니다. 이와 관련된 유명한 몇몇 구조에 대해 알아보겠습니다.
ResNet
Residual block은 image classification을 위한 convolutional networks에 처음 사용됐습니다. 결과적으로 residual network, ResNets이 나오게 됐습니다.

ResNet에선 각 residual block은 batch normalization operation, ReLU activation, convolutional layer를 포함합니다. input를 다시 추가하기전에 같은 sequence로 이어집니다. 이런 operation 순서는 image classification에서 잘 작동한다고 합니다.

매우 깊은 네트워크에선, parameter의 갯수는 바람직하지 않게 매우 커질 것입니다. 'Bottleneck residual blocks'은 3개의 convolution을 사용해서 parameter를 조금 더 효율적으로 쓸 수 있도록 합니다.
첫번째 convolution은 1x1 kernel을 갖고 channel의 수를 줄입니다.
두번째 convolution은 3x3 kernel이며, 세번째 convolution은 channel의 수를 원래대로 증가시키기 위한 또다른 1x1 kernel이 존재합니다. 이런 방법을 사용하면, 더 적은 parameter를 사용해 3x3 pixel에 대한 information을 통합할 수 있습니다.

ResNet-200 model은 200개의 layer를 갖는 ImageNet database의 image classification을 위한 모델입니다. 구조는 AlexNet와 VGG와 비슷하지만 vanilla convolutional layers 대신 'bottleneck residual block'을 사용합니다. AlexNet과 VGG에선, 점차적으로 spatial resolution이 줄어들며 분산되고 동시에 channel의 수는 증가합니다. 여기서 resolution은 stride가 2인 convolution을 사용한 downsampling에 의해 줄어듭니다. channel의 수는 representation에 0을 추가하거나 추가적인 1x1 convolution을 사용해 증가됩니다. network의 시작은 7x7 convolutional layer이고, 그 다음 downsampling operation이 진행됩니다. 마지막엔, fully conntected layer가 길이가 100인 vector에 block을 mapping합니다. 이는 class probability를 생성하기ㅣ 위해 softmax layer을 통해 지나갑니다.
ResNet-200의 에러는 (4.8%,20.1%)에 도달해, human performance를 능가하는 최초의 model입니다. 그러나 이 모델은 2016년의 SOTA이고, 현재는 9.0% error에 달하는 모델이 있습니다. 이는 다음 챕터에서 배울 transformer를 기반으로 생성된 모델입니다.
DenseNet
기존의 residual block은 이전 layer로부터 나온 output을 받고, 몇몇의 network layer를 거쳐 패스하고, original input에 다시 추가하는 방식이였습니다. 여기선 수정된 것과 기존의 것을 concat하는 방법을 사용했습니다. 이 방법은 representation size가 증가하지만 (conv net에선 channel을 의미), 선택적인 subsequent linear transformation은 기존의 size에 다시 mapping할 수 있다는 장점이 있습니다. (1x1 convolution)
물론 이 방법은 representation을 같이 추가할 수 있고, weigthed sum을 취하거나, 조금 더 복잡한 방식으로 결합할 수 있습니다.
DenseNet에선 concat을 사용해, layer에 들어가는 input은 모든 이전의 layer들로부터 concatenated output을 구성하게 됩니다. (?) 이것들은 그 자체가 이전의 representation과 연결돼 다음 layer로 전달되는 새로운 represenation을 생성하도록 처리됩니다. 이 concat은 이전 layer에서 outpu에 직접적으로 contribution 하기 때문에 loss fuction이 합리적으로 동작한다는 것을 의미합니다.
U-Nets , hourglass networks

이 model은 encoder--decoder 구조를 가집니다. encoder는 receptive field가 커질때까지 반복적으로 image를 downsample하고 information은 image로부터 통합됩니다. decoder는 다시 original image 사이즈로 다시 upsample을 합니다. 마지막 output은 각 pixel에 대해 가능한 object class에 대한 proabability가 됩니다. 이 구조의 단점은 network 중간의 낮은 resolution representation은 마지막 결과를 정확하게 만들기 위해 high-resolution의 detail을 기억하고 있어야 합니다. 만약 residual connection이 encoder에서 짝꿍(적절한) decoder로 representation을 전송한다면 위의 단점을 극복할 수 있습니다.
U-net은 earlier representation이 later representation에 concat되는 encoder-decoder 구조입니다.
original implementation은 "valid" representation을 사용해, spatial size가 3x3 convoltuional layer를 적용해 2 pixel에 의해 줄어듭니다. 이는 upsampled version이 encoder에 대응하는 부분보다 더 작다는 것을 의미하고, concat하기 전에 crop되어야 합니다. 충분한 implementation은 zero padding을 사용하면, crop을 안해도 됩니다. "U-Net은 completely convolution이기 때문에, training 이후엔, image가 어떤 사이즈여도 가능합니다"
hourglass networks
hourglass network는 u-net과 비슷하지만 skip connection에 추가적인 convolutional layer를 적용하고 이를 concat하기 보단 decoder에 결과를 추가하는 방식으로 동작합니다. 이 model의 series는 'stacked hourglass network'를 형성하고 image를 local 단계와 global 단계 사이에서 고려해줍니다. 이런 network는 'pose estimation'에 쓰이고, system은 각 joint의 "heatmap"을 예측하도록 훈련됩니다. 그리고 estimated position은 각 heat map의 maximum이 됩니다.
Why do nets with residual connections perform so well?
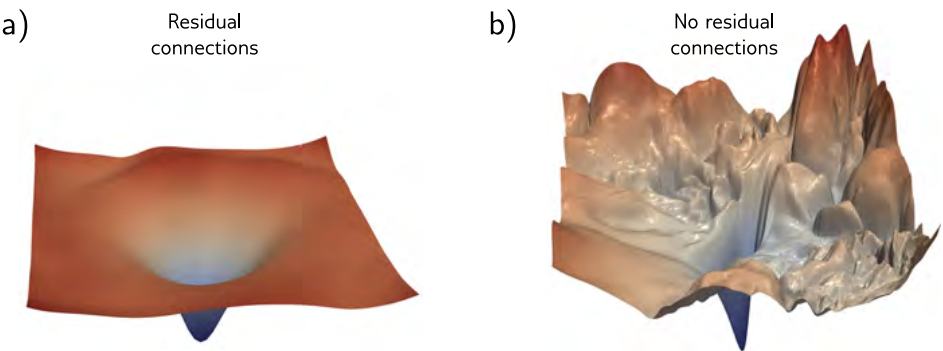
Residual net은 더 깊은 network가 학습될 수 있도록 해줍니다. ResNet 구조에선 1000개의 layer로 확장해도 효과적으로 훈련할 수 있습니다. image classification의 성능 향상은 추가적인 network depth로 야기됐지만, 2가지의 이유로 이 viewpoint는 상충됩니다.
1. 더 얕고 넓은 residual network는 가끔 더 깊고 좁은 것보다 성능이 좋습니다. 즉, 가끔은 더 적은 layer 이면서 layer당 더 많은 channel일 때 성능이 더 좋을 수 있습니다. (layer는 얕고 channel은 많을 때)
2. 훈련하는 동안 gradient는 unraveled network에서 매우 긴 path를 통해 효과적으로 늘지 않습니다. 매우 깊은 network는 결국 더 얕은 network의 combination처럼 행동할 것입니다.
deeper network가 훈련되는 한, residual connection은 그 자체로 value를 추가할 것입니다. 이 관점은 residual network의 loss surface의 minimum 주변은 (skip connection이 제거된 똑같은 network와 비교했을 때) 더 smooth하고 더 예측가능한 경향이 있다는 점에 근거합니다. 이는 generalize를 더 잘하는 좋은 solution을 학습하기 쉽도록 만듭니다.
Summary
network depth를 늘리는 것은 image classification task에서 막연히 training과 test performance 모든 면에서 성능을 감소시킵니다. 초기의 parameter에 대한 loss의 gradient가 빠르고 예측불가능하게 바뀌기 때문입니다. residual connection은 진행된 representation에 input을 다시 추가하는 것입니다. 각 layer는 간접적일 뿐만 아니라 output에 직접적으로 기여할 수 있기 때문에, 많은 layer를 통해 gradient를 전파하는 것이 필수 사항이 아니고, loss surface는 더 매끄러워집니다. 그렇기 대문에 residual net은 vanishing gradient 문제로부터 벗어날 수 있지만 forward propagation 동안 activation의 variance가 기하급수적으로 늘어나는 단점이 잇습니다. 이 문제는 batch normalization을 추가함으로써 해결할 수 있고, 이 방법은 batch의 empirical mean과 variance를 보완하고 학습된 parameter를 이용해 shift하고 rescale하게 됩니다. 만약 parameter가 적절하게 초기화된다면, 매우 깊은 network도 학습될 것입니다.
residaul link & batch normalization이 loss surface를 더 매끈하게 한다는 증거가 존재하고, 그렇다면 우리는 더 큰 learning rate를 사용할 수 있습니다. 나아가, batch statistics의 variability는 regularization의 source를 추가합니다.
residual block은 convolutional network에 포함되어 왔습니다. 이 method는 더 깊은 network가 image classification performance에서 알맞게 증가하며 훈련할 수 있도록 합니다. residual net의 variation은 DenseNet architecture을 포함하고, 현재 layer에 이전의 모든 layer의 output을 concat합니다. U-Net에선, encoder-decoder model에 residual connection을 추가한 방법입니다.
'Artificial Intelligence > Deep Learning' 카테고리의 다른 글
| 13. Unsupervised learning (0) | 2024.05.07 |
|---|---|
| 12. Graph neural networks (1) | 2024.05.03 |
| 11. Transformers (0) | 2024.04.23 |
| 9. Convolutional networks (0) | 2024.04.16 |
| 8. Regularization (0) | 2024.04.15 |



